C语言课程设计-校园导游系统

C语言课程设计-校园导游系统

邱海梦旌 Lv1
  2023-01-16 15:45:38 2023-01-16 15:45:38 创建   2024-12-09 23:01:23 2024-12-09 23:01:23 更新      4.8k 字  21 分钟  

序言

  本篇文章的目的是记录下我设计并实现《 C 校园导游系统》的过程，其实我本来想要把这个系统做的很好，但是奈何本学期出现了一些突发事件，导致时间精力都很有限，所以只能暂时搁置了。
  选择这个项目的初心是为了锻炼自己，但最终我在它身上只花费了3天时间，作为达到数据结构课程设计的要求它是完全满足的，但是对我而言离我想象中的要求还差得远，就像它只是一个游戏demo，并不是成品。
  那为什么我还要拿出来做文章呢？我能力有限无法真正完成它，大概率以后也没时间去做它了，但是记录下万一哪天用上了呢，当然也可以给后辈一个参考价值吧。
  不多说了，现在进入正题吧。

需求分析

  • 提供直观的学校地图界面供用户进行查看，以点作为景点，以边作为道路；

  • 提供景点相关信息查询功能，能够查询景点位置和输出景点的相关信息；

  • 提供问路查询功能，用户只需输入起点和终点，系统就会为用户提供最短路径；

  • 提供景点类型查询功能，用户可查询相关类型建筑及其信息；

  • 总结：《校园导游咨询系统》需要为用户提供一个可视化的校园平面图，并且提供景点查询功能和最短路径查询功能，满足用户的对校园导游系统的基本需求。

设计过程

地图设计

要制作导游系统，首先就是明确我们的导游范围，为了明确如何画出地图，我查看了我们学校的地图。
玉溪师范学院地图
然后根据地图筛选出了15个景点建筑加入到了这次的系统地图中。
将15个地点抽象出来构成图结构

1.东北门 2.大学生活动中心 3.实训大楼A 4.滋味苑 5.龙马公寓 6.后山 7.学生宿舍F,G幢 8.学生宿舍K,L,M,N幢 9.主教学区 10.品味苑 11.艺术综合楼 12.图书馆 13.运动场 14.东南门 15.传习馆

OK,就这样一份地图模板就制作好了，也可以说图结构的顶点确定好了，那么接下来就是确定边权值。
测量边权值的方法，我这里我采用高德地图的测距小工具，几分钟就全部测量好了，将测量好的数据保存起来，之后用得到。

接下来就将地图写入到系统中，就纯靠 printf 画图了
现在我们的地图模块就设计好了。但是现在只是一个没有任何信息的图，之后还将导入景点编号、景点信息、边权值。

创建数据结构并初始化

将我们测量好的数据保存于相应的.txt文件中，这里我将景点编号保存在Number.txt文件，景点名称保存在Name.txt文件，景点信息保存在info.txt文件，各两点间的距离（边权值）保存在Distance.txt文件。

然后创建我们所需的数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#define N 15				//顶点数目值
#define M 22				//边数目值
#define VexType string		//顶点数据类型
#define EdgeType int		//边数据类型
#define INF 0x3f3f3f3f		//作为最大值

//景点数据结构
typedef struct Spot
{
	int number;
	char name[20];
	char SpotInfo[50];
}Spot;

//图的数据结构
typedef struct Graph
{
	VexType V[N];		//顶点表
	EdgeType E[N][N];	//边表
	int vnum, ednum;	//顶点数、边数
}Graph;

初始化

1
2
3
4
5
6
7
8
9
10
11
//初始化图的顶点表，邻接矩阵等
void InitGraph(Graph& G)
{
	//初始化边表
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			G.E[i][j] = INF;
		}
	}
	G.ednum = G.vnum = 0;	//初始化顶点数、边数
}

插入顶点和边

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//插入点函数，改变顶点表
void InsertNode(Graph& G, VexType v)
{
	if (G.vnum < N)
	{
		G.V[G.vnum++] = v;
	}
}

//插入边函数，改变邻接矩阵
void InsertEdge(Graph& G, VexType v, VexType w, int weight)
{
	int p1, p2;
	p1 = p2 = -1;
	for (int i = 0; i < G.vnum; i++)
	{
		if (G.V[i] == v)p1 = i;
		if (G.V[i] == w)p2 = i;
	}
	if (p1 != -1 && p2 != -1)
	{
		G.E[p1][p2] = G.E[p2][p1] = weight;	//无向图邻接矩阵对称
		G.ednum++;
	}
}

创建图，读取文件导入数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//创建图功能实现函数
void CreatGraph(Graph& G)
{
	int vn, an;	//顶点数，边数
	vn = N;
	an = M;
	int count = 0;
	char str1[20], str2[20];
	string s1, s2;
	int temp = 0;
	FILE* fp1 = fopen("Number.txt", "r");
	FILE* fp2 = fopen("Distance.txt", "r");
	if (fp1 == NULL && fp2 == NULL)
	{
		printf("打开文件失败！\n");
		exit(0);
	}
	//从文件中读取景点编号
	for (int i = 0; i < N; i++)
	{
		count = fscanf(fp1, "%s", str1);
		if (count == -1)exit(0);
		s1 = str1;
		InsertNode(G, s1);
	}
	//从文件中读取所有边的权值
	for (int i = 0; i < M; i++)
	{
		count = fscanf(fp2, "%s %s %d", str1, str2, &temp);
		if (count == -1)exit(0);
		s1 = str1;
		s2 = str2;
		InsertEdge(G, s1, s2, temp);
	}
	fclose(fp1);
	fclose(fp2);
}

到这里我们的图就创建完成了

Dijkstra算法

无论是在教材还是各类算法书籍中都少不了的最短路径算法Dijkstra算法，是由荷兰计算机科学家 Edsger Wybe Dijkstra 在1956年发现的算法，戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。Dijkstra 算法原始版本仅适用于找到两个顶点之间的最短路径，后来更常见的变体固定了一个顶点作为源结点然后找到该顶点到图中所有其它结点的最短路径，产生一个最短路径树。本算法每次取出未访问结点中距离最小的，用该结点更新其他结点的距离。

核心思想：按路径长度递增次序产生算法，将图数据结构分为顶点集V和边集E，接下来初始化图的顶点表和邻接矩阵，将所有边的权值设置为无穷大，然后插入点改变顶点表，插入边改变邻接矩阵。之后从第一个顶点开始计算最短路径，假如该顶点与其他顶点有边连接，则将其边权值加入到最短路径集，然后依次比较，最后选出最小的边权值，并记录前驱，然后从前驱开始又执行边权值的比较，直到最后到达终点结束，最短路径值即之前记录过的前驱的边权值相加的最终结果。

这样讲还是难懂，那我们从头开始了解Dijkstra算法吧

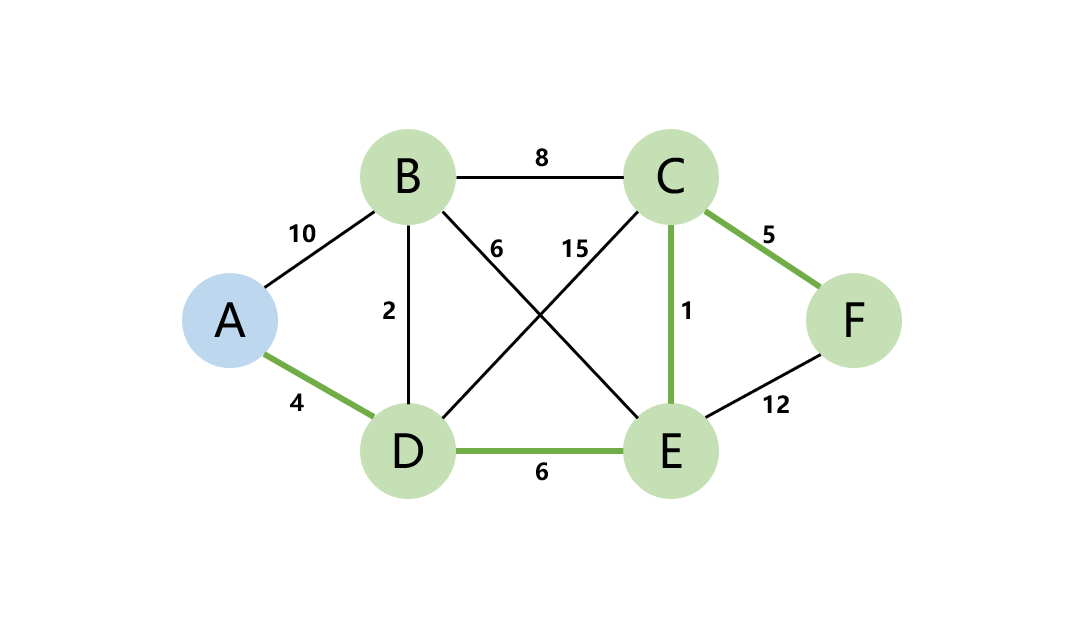
下面以该图为例讲解Dijkstra算法寻找最短路径的过程

以A为起始点，求A到BCDEF的最短路径

要求A到其他5个点的最短距离，我们构造一个数组记录A到BCDEF5个点的路径距离。

需要注意的是

  • 如果A能够直接到达节点，则使用路径长度，即边权值作为其距离。
  • 如果A节点不能够直接到达节点则用无穷大表示A到该点的距离。
  • 任何点到自身的距离都为0

在最开始A到其余点的数组如下

A B C D E F
0 10 ∞ 4 ∞ ∞

Dijkstra算法的思想是：从以上最短距离数组中每次选择一个最近的点，将其作为下一个点，然后重新计算从起始点经过该点到其他所有点的距离，并更新最短距离的值，已经选取过的点就是确定了最短路径的点，不再参与下一次计算。

我们来看看实际的选取过程

第一次选取

构建好的数组是这样的

A B C D E F
0 10 ∞ 4 ∞ ∞
第一步选取该最短路径数组中值最小的一个点。因为A点到本身不需要参与运算，所以从剩下的点中选择最短的一个是D。
第二步以A-D的距离为最近距离更新A点到所有点的距离。即相当于A点经过D点，计算A到其他点的距离。


A-A: 0
A-B: A-D-B:6
A-C: A-D-C:19
A-D: A-D:4
A-E: A-D-E:10
A-F: A-D-F:∞

将现在A到各个点的距离和之前相比较，取最小值，更新BCE的距离，得到新的最短距离数组

A B C D E F
0 6 19 4 10 ∞

第二次选取

AD两点已经选取，不再参与下面的计算。

A B C D E F
0 6 19 4 10 ∞

以B为最新点，更新最短距离数组

A-A: 0
A-B: A-D-B:6
A-C: A-D-B-C:14
A-D: A-D:4
A-E: A-D-B-E:12
A-F: A-D-B-F:∞

对比现在的最短距离和上一个数组的距离，到相同节点选最小的，更新最短距离数组。
C点由19更新成14，E点走A-D-E为10，距离更短所以不更新，得到如下数组：

A B C D E F
0 6 14 4 10 ∞

第三次选取

第一步：选取除了A B D节点之外的剩余节点中最短节点，为点E
第二步：以E点为最新节点，更新最短路径数组
因为在上一步中计算达到E点的距离时没有更新距离，A-D-E 为10 最短，所以更新E点到B C F点的距离时走的路径是A-D-E。注意这里的最短距离有对应的路径，选择最小值就是选择最短距离。

A-A: 0
A-B: A-D-B:6
A-C: A-D-E-C:11
A-D: A-D:4
A-E: A-D-E:10
A-F: A-D-E-F:22
对比现在的最短距离和上一个数组的距离，到相同节点选最小的，更新最短距离数组。
更新C点走A-D-E-C为11，比之前的A-D-B-C 14距离更近，更新到F点距离，得到如下数组：

A B C D E F
0 6 11 4 10 22

第四次选取

第一步：选取除了A B D E节点之外的剩余节点中最短节点，为点C
第二步：以C点为最新节点，更新最短路径数组

A-A: 0
A-B: A-D-B:6
A-C: A-D-E-C:11
A-D: 4
A-E: A-D-E:10
A-F: A-D-E-C-F:16
对比现在的最短距离和上一个数组的距离，到相同节点选最小的，更新最短距离数组。
更新到F点距离，可以得到如下数组：

A B C D E F
0 6 11 4 10 16

第五次选取

第一步：选取除了A B C D E节点之外的剩余节点中最短节点，也就是最后一个节点：F
第二步：以F点为最新节点，更新最短路径数组。由于F点是最后一个点，所以也不用更新数组，目前的数组就是所求数组将F点加入最短路径范围中，此时所有的点都加入了最短路径范围，也就是说A点到所有点的距离都找到了。最终得出的距离值为：

最终得到的结果为：

A B C D E F
0 6 11 4 10 16

最终结果

A B C D E F
0 6 11 4 10 16

A-A: 0

A-B: A-D-B:6

A-C: A-D-E-C:11

A-D:4

A-E: A-D-E:10

A-F: A-D-E-C-F:16

代码实现Dijkstra算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#define INF 0x3f3f3f3f	//作为最大值

//Dijkstra算法全局变量
bool S[N];	//顶点集
int D[N];	//到各个顶点的最短路径
int Pr[N];	//记录前驱

void Dijkstra(Graph G, int v)
{
	//初始化
	int n = G.vnum;	//n为图的顶点个数
	for (int i = 0; i < n; i++)
	{
		S[i] = false;
		D[i] = G.E[v][i];
		if (D[i] < INF)
		{
			Pr[i] = v;	//v与i连接，v为前驱
		}
		else
		{
			Pr[i] = -1;
		}
	}
	S[v] = true;
	D[v] = 0;
	//初始化结束，求最短路径，并加入S集
	for (int i = 1; i < n; i++)
	{
		int min = INF;
		int temp;
		for (int w = 0; w < n; w++)
		{
			if (!S[w] && D[w] < min)		//某点temp未加入S集，且为当前最短路径
			{
				temp = w;
				min = D[w];
			}
		}
		S[temp] = true;
		//更新从源点出发至其余点的最短路径 通过temp
		for (int w = 0; w < n; w++)
		{
			if (!S[w] && D[temp] + G.E[temp][w] < D[w])
			{
				D[w] = D[temp] + G.E[temp][w];
				Pr[w] = temp;
			}
		}
	}
}

//输出最短路径
void Path(Graph G, int v)
{
	if (Pr[v] == -1)
	{
		return;
	}
	Path(G, Pr[v]);
	cout << G.V[Pr[v]] << "->";
}

导游系统问路查询功能

在了解以及实现了Dijkstra算法之后，我们还要在程序中调用它。

  • 用户只需输入起点和终点，系统就会为用户提供最短路径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
//调用最短路径-Dijkstra算法
void Shortest_Dijkstra(Graph& G)
{
	string vname;
	string vnamed;
	int v1, v2;
	char ch = '1';

	while (true)
	{
		v1 = -1;
		v2 = -1;
		cout << "请输入起点编号：";
		cin >> vname;
		for (int i = 0; i < G.vnum; i++) {
			if (G.V[i] == vname)
			{
				v1 = i;
			}
		}
		if (v1 == -1)
		{
			cout << "没有找到输入点！" << endl;
			system("pause");
			system("cls");
			drawMap();
			continue;
		}
		cout << "请输入终点编号：";
		cin >> vnamed;
		for (int i = 0; i < G.vnum; i++) {
			if (G.V[i] == vnamed)
			{
				v2 = i;
			}
		}
		if (v2 == -1)
		{
			cout << "没有找到终点！" << endl;
			system("pause");
			system("cls");
			drawMap();
			continue;
		}
		Dijkstra(G, v1);
		cout << "\n目标点" << "\t" << "最短路径值" << "\t" << "最短路径" << "\t" << endl;
		for (int i = 0; i < G.vnum; i++)
		{
			if (i != v1 && i == v2)
			{
				cout << " " << G.V[i] << "\t" << D[i] << "米" << "\t" << "\t";
				Path(G, i);
				cout << G.V[i] << endl;
			}
		}
	}
}

效果展示:

1
2
3
4
5
请输入起点编号：1
请输入终点编号：5

目标点  最短路径值      最短路径
 5      400米           1->2->4->5

导游系统信息查询功能

信息查询功能很简单，把预先准备的景点信息文件读取到程序的景点数据结构中，然后输出它就行了。

部分代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
void NameFile(Spot spt[])
{
	int count = 0;
	int i;
	FILE* fp = fopen("Name.txt", "r");

	if (fp == NULL) {
		printf("打开文件失败！\n");
		exit(0);
	}
	for (i = 0; i < N; i++) {
		spt[i].number = i + 1;
		count = fscanf(fp, "%s", spt[i].name);
		if (count == -1) exit(0);
		//printf("%s\n", spt[i].name);		测试代码
	}
	fclose(fp);
}

void InfoFile(Spot spt[])
{
	int count = 0;
	int i;
	FILE* fp = fopen("Info.txt", "r");

	if (fp == NULL) {
		printf("打开文件失败！\n");
		exit(0);
	}
	for (i = 0; i < N; i++) {
		count = fscanf(fp, "%s", spt[i].SpotInfo);
		if (count == -1)exit(0);
		//printf("%s\n", spt[i].SpotInfo);		测试代码
	}
	fclose(fp);
}

void printInfo(Spot spt[], int i)
{
	printf("\n%d.%s\n简介：%s\n", spt[i].number, spt[i].name, spt[i].SpotInfo);
}

导游系统景点类型查询功能

功能分析：

  • 1个景点类型包含若干个景点
  • 用户可以查询该景点类型包含哪几个景点
  • 用户可以详细了解某一个景点的信息

首先我们初始化景点类型数据结构，然后将各个景点进行类型分类，然后加入景点类型查询模块，后面嵌套一下景点信息查询模块。

部分代码展示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
#define TN 5				//类型数目值

//景点类型数据结构
typedef struct SpotType
{
	string typeName;
	Spot S[TN];
	int number;
}SpotType;

//初始化景点类型数据结构
void BuildingType(Spot spt[], SpotType stype[])
{
	stype[0].typeName = "教学楼";
	stype[1].typeName = "学生宿舍";
	stype[2].typeName = "食堂";
	stype[3].typeName = "课外活动点";
	stype[0].S[0] = spt[2];
	stype[0].S[1] = spt[8];
	stype[0].S[2] = spt[10];
	stype[0].number = 3;
	stype[1].S[0] = spt[4];
	stype[1].S[1] = spt[6];
	stype[1].S[2] = spt[7];
	stype[1].number = 3;
	stype[2].S[0] = spt[3];
	stype[2].S[1] = spt[9];
	stype[2].number = 2;
	stype[3].S[0] = spt[1];
	stype[3].S[1] = spt[5];
	stype[3].S[2] = spt[12];
	stype[3].S[3] = spt[14];
	stype[3].number = 4;
}

//查询景点类型
void ShowType(Spot spt[], SpotType stype[])
{
	int select = 0;

	while (true)
	{
		cout << "                                                    |==============================|" << endl;
		cout << "                                                    |          1." << stype[0].typeName << "            |" << endl;
		cout << "                                                    |          2." << stype[1].typeName << "          |" << endl;
		cout << "                                                    |          3." << stype[2].typeName << "              |" << endl;
		cout << "                                                    |          4." << stype[3].typeName << "        |" << endl;
		cout << "                                                    |==============================|" << endl;
		cout << "请选择你需要您要了解的类型：";
		cin >> select;
		getchar();
		switch (select)
		{
		case 1:
			Print_Type(stype[select - 1]);
			break;
		case 2:
			Print_Type(stype[select - 1]);
			break;
		case 3:
			Print_Type(stype[select - 1]);
			break;
		case 4:
			Print_Type(stype[select - 1]);
			break;
		default:
			cout << "请输入有效选项！\n回车键继续..." << endl;
			getchar();
			system("cls");
			drawMap();
			continue;
		}
		cout << "\n您需要了解以上建筑信息吗？（输入1了解，输入0取消）：";
		int select2;
		int select3;
		while (true)
		{
			cin >> select2;
			if (select2 == 1)
			{
				while (true)
				{
					cout << "\n请输入你想要了解建筑的编号（输入0取消）：";
					cin >> select3;
					if (select == 1)
					{
						if (select3 == 3 || select3 == 9 || select3 == 11)
						{
							printInfo(spt, select3 - 1);
						}
						else if (select3 == 0)
						{
							break;
						}
						else
						{
							cout << "请输入正确的此类型建筑编号！" << endl;
						}
					}
					else if (select == 2)
					{
						if (select3 == 5 || select3 == 7 || select3 == 8)
						{
							printInfo(spt, select3 - 1);
						}
						else if (select3 == 0)
						{
							break;
						}
						else
						{
							cout << "请输入正确的此类型建筑编号！" << endl;
						}
					}
					if (select == 3)
					{
						if (select3 == 4 || select3 == 10)
						{
							printInfo(spt, select3 - 1);
						}
						else if (select3 == 0)
						{
							break;
						}
						else
						{
							cout << "请输入正确的此类型建筑编号！" << endl;
						}
					}
					if (select == 4)
					{
						if (select3 == 2 || select3 == 6 || select3 == 13 || select3 == 15)
						{
							printInfo(spt, select3 - 1);
						}
						else if (select3 == 0)
						{
							break;
						}
						else
						{
							cout << "请输入正确的此类型建筑编号！" << endl;
						}
					}
				}
			}
			else if (select2 == 0)
			{
				break;
			}
			else
			{
				cout << "请输入正确选项！" << endl;
				break;
			}
			if (select3 == 0) break;
		}
	}
}

总结

本次的校园导游系统是我的数据结构课程设计，希望这篇文章能够帮我记下Dijkstra算法的实际运用，今后遇到相应的算法也能够有解决思路。

本次的导游系统介绍就到这了，有需要看源代码的朋友可以到我的 GitHub 仓库中查看。

链接：

校园导游系统

本章一句：
当你因为错过太阳而哭泣的时候，你也要错过群星了。——泰戈尔《飞鸟集》

  • 标题: C语言课程设计-校园导游系统
  • 作者: 邱海梦旌
  • 创建于 : 2023-01-16 15:45:38
  • 更新于 : 2024-12-09 23:01:23
  • 链接: https://blog.invictusqiu.top/2023/01/16/CampusGuideSystem/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
目录
C语言课程设计-校园导游系统
  1. 序言
  2. 需求分析
  3. 设计过程
    1. 地图设计
    2. 创建数据结构并初始化
    3. Dijkstra算法
      1. 第一次选取
      2. 第二次选取
      3. 第三次选取
      4. 第四次选取
      5. 第五次选取
      6. 最终结果
    4. 代码实现Dijkstra算法
    5. 导游系统问路查询功能
    6. 导游系统信息查询功能
    7. 导游系统景点类型查询功能
  4. 总结
  5. 链接：